def len_of_string(s):
if s == '':
return 0
return 1 + len_of_string(s[1:])
len_of_string('hello')5Recursion is a method of solving problems that involves breaking a problem down into smaller and smaller subproblems until you get to a small enough problem that it can be solved trivially. Usually recursion involves a function calling itself. While it may not seem like much on the surface, recursion allows us to write elegant solutions to problems that may otherwise be very difficult to program.
length(s)={01+length(s[1:])if s=”otherwise
Let’s execute this function on the string “hello”.
length("hello")=1+length("ello")=1+1+length("llo")=1+1+1+length("lo")=1+1+1+1+length("o")=1+1+1+1+1+length("")=1+1+1+1+1+0=5
n!={1(n−1)!×nif n=0(base case)if n>0(recursive case)
Let’s execute the factorial function for n=3: 3!=3×2!=3×2×1!=3×2×1×0!=3×2×1×1=6
isPalindrome(s)=⎩⎨⎧TrueFalseisPalindrome(s[1:−1])if s=”(base case)if s[0]=s[−1](base case)if s[0]=s[−1](recursive case)
Executing the function for s=’racecar’: isPalindrome(’racecar’)=isPalindrome(’aceca’)=isPalindrome(’cec’)=isPalindrome(’e’)=isPalindrome(”)=True
For s=’oello’: isPalindrome(’oello’)=isPalindrome(’ell’)=False

How to move all disks from the leftmost peg to the rightmost peg?
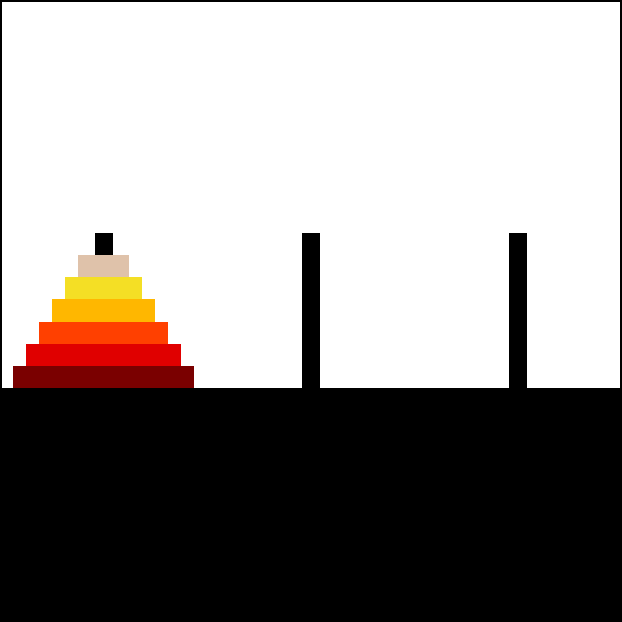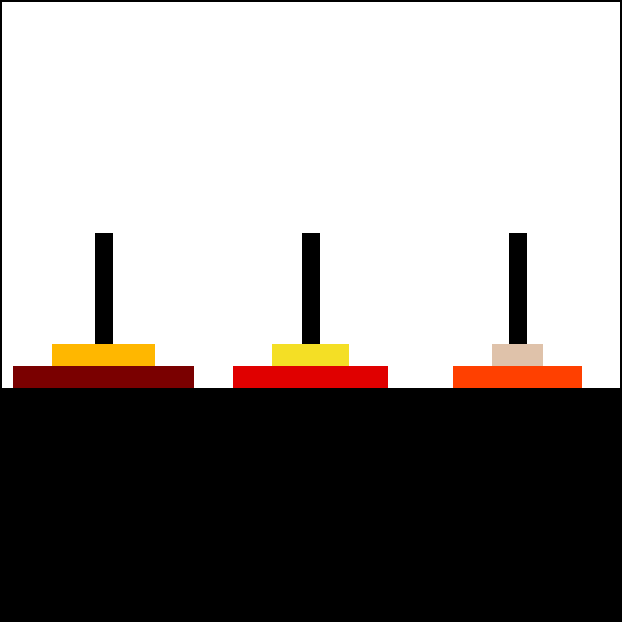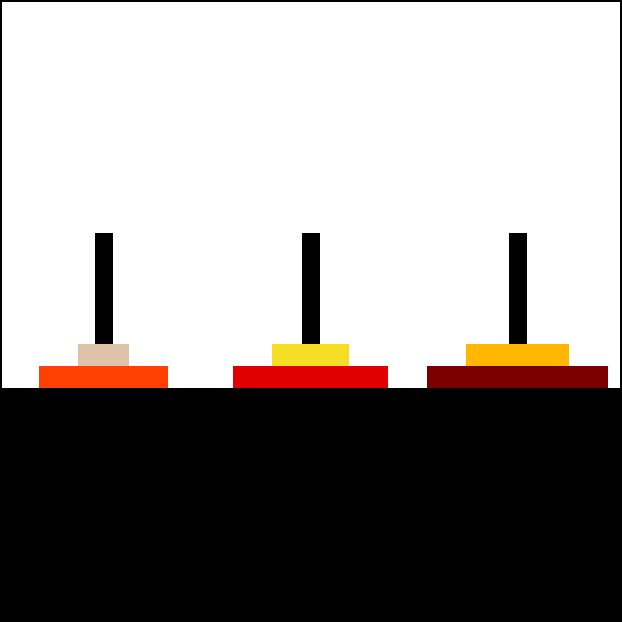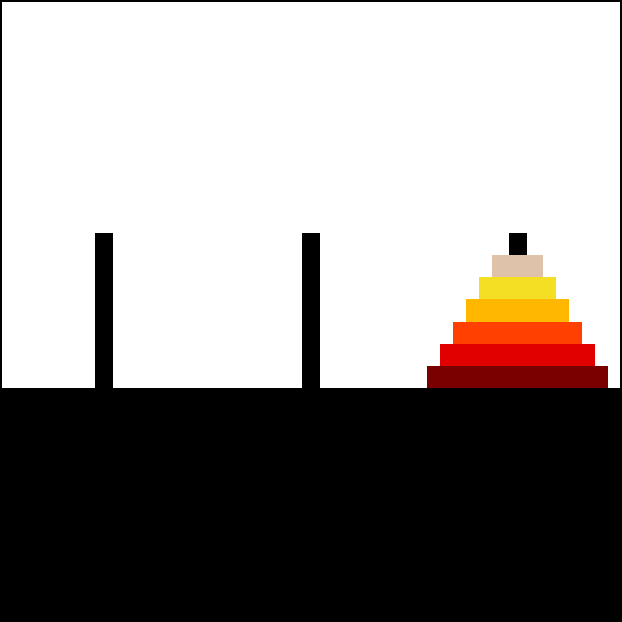
hanoi(n,from,to,via)=⎩⎨⎧do nothinghanoi(n−1,from,via,to)move disk from from to tohanoi(n−1,via,to,from)if n=0(base case)if n>0(recursive case)if n=1(base case)if n>0(recursive case)
Move disk from A to C
Move disk from A to B
Move disk from C to B
Move disk from A to C
Move disk from B to A
Move disk from B to C
Move disk from A to CGCD is the largest positive integer that divides the numbers without a remainder.
It can be computed using the following recursive algorithm (Euclid’s algorithm): gcd(a,b)={agcd(b,amodb)if b=0(base case)if b>0(recursive case)
How to calculate xn efficiently?
The naive approach is to multiply x by itself n times. O(n)
power(x,n)={1x×power(x,n−1)if n=0(base case)if n>0(recursive case)
But we can do better in O(logn) time. power(x,n)=⎩⎨⎧1power(x2,n/2)x×power(x2,(n−1)/2)if n=0(base case)if n is even(recursive case)if n is odd(recursive case)
Given a sorted array A and a value x, how to find if x is in A?
If we check every element in A, we can find x in O(n) time.
But we can do better in O(logn) time.
binarySearch(A,x,low,high)=⎩⎨⎧FalseTruebinarySearch(A,x,low,mid−1)binarySearch(A,x,mid+1,high)if low>high(base case)if A[mid]=x(base case)if A[mid]>x(recursive case)if A[mid]<x(recursive case)
def binary_search(a, x, low, high):
if low > high:
return False
else:
mid = (low + high) // 2
if a[mid] == x:
return True
elif a[mid] < x:
return binary_search(a, x, mid + 1, high)
else:
return binary_search(a, x, low, mid - 1)
a = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print(binary_search(a, 5, 0, len(a)-1))
print(binary_search(a, 10, 0, len(a)-1))True
False
mergeSort(A)={Amerge(mergeSort(A[:mid]),mergeSort(A[mid:]))if len(A)≤1(base case)if len(A)>1(recursive case)
merge(A,B)=⎩⎨⎧ABmin(A[0],B[0]) + merge(A[1:],B)min(A[0],B[0]) + merge(A,B[1:])if len(B)=0(base case)if len(A)=0(base case)if A[0]<B[0](recursive case)if A[0]≥B[0](recursive case)
def merge(a, b):
# recursive merge
if len(a) == 0:
return b
elif len(b) == 0:
return a
else:
if a[0] < b[0]:
return [a[0]] + merge(a[1:], b)
else:
return [b[0]] + merge(a, b[1:])
def merge_sort(a):
if len(a) <= 1:
return a
else:
mid = len(a) // 2
return merge(merge_sort(a[:mid]), merge_sort(a[mid:]))
a = [1, 3, 5, 7, 9, 2, 4, 6, 8, 10]
print(merge_sort(a))[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.

The pseudocode for DFS is as follows: - Mark the current vertex as being visited. - Explore each adjacent vertex that is not included in the visited set.
dfs(G,v)={do nothingmark v as visited and dfs(G,w)if v is visited(base case)for each w adjacent to v(recursive case)
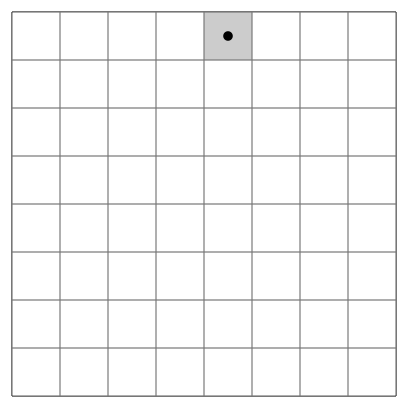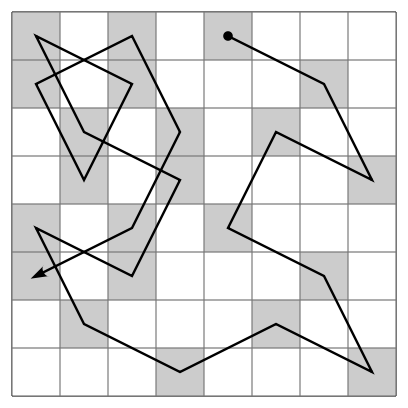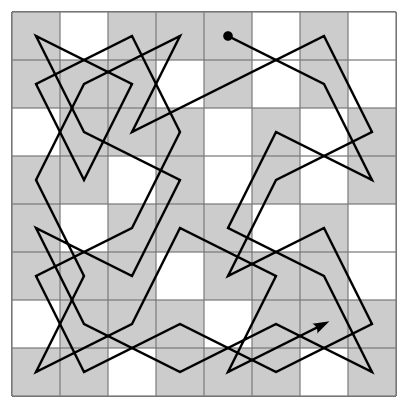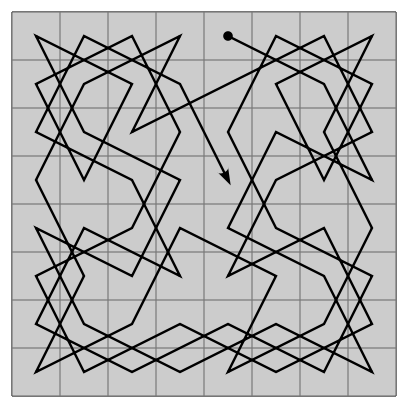
Problem: Given a chess board of size n×n and a starting position (x,y), find a sequence of moves of a knight that visits every square exactly once.
knightTour(n,x,y,visited)=⎩⎨⎧StopFalseFalseTrueTrueTrueTrueTrueTrueTrueTrueif visited=n2(base case)if x or y is out of bounds(base case)if (x,y) is already visited(base case)if knightTour(n,x+1,y+2,visited+1)(recursive case)if knightTour(n,x+1,y−2,visited+1)(recursive case)if knightTour(n,x−1,y+2,visited+1)(recursive case)if knightTour(n,x−1,y−2,visited+1)(recursive case)if knightTour(n,x+2,y+1,visited+1)(recursive case)if knightTour(n,x+2,y−1,visited+1)(recursive case)if knightTour(n,x−2,y+1,visited+1)(recursive case)if knightTour(n,x−2,y−1,visited+1)(recursive case)
def knight_tour(n, x, y, visited):
# print the path
if len(visited) == n * n:
print(visited)
return True, visited
else:
for dx, dy in [(1, 2), (2, 1), (-1, 2), (-2, 1),
(-1, -2), (-2, -1), (1, -2), (2, -1)]:
nx, ny = x + dx, y + dy
if nx >= 0 and nx < n and ny >= 0 and ny < n and (nx, ny) not in visited:
visited.append((nx, ny))
res, visited = knight_tour(n, nx, ny, visited)
if res:
return True, visited
visited.pop()
return False, visited
res, path = knight_tour(5, 0, 0, [(0, 0)])
print()
# visualize the path just by putting numbers on the board
board = [[0] * 5 for _ in range(5)]
for i, (x, y) in enumerate(path):
board[x][y] = i + 1
for row in board:
print(row)[(0, 0), (1, 2), (2, 4), (0, 3), (1, 1), (3, 0), (4, 2), (3, 4), (2, 2), (4, 3), (3, 1), (1, 0), (0, 2), (1, 4), (3, 3), (4, 1), (2, 0), (0, 1), (1, 3), (2, 1), (4, 0), (3, 2), (4, 4), (2, 3), (0, 4)]
[1, 18, 13, 4, 25]
[12, 5, 2, 19, 14]
[17, 20, 9, 24, 3]
[6, 11, 22, 15, 8]
[21, 16, 7, 10, 23]
Problem: Given a partially filled sudoku board, fill the empty cells.
def is_valid(board, x, y):
n = len(board)
# check row
for j in range(n):
if j != y and board[x][j] == board[x][y]:
return False
# check column
for i in range(n):
if i != x and board[i][y] == board[x][y]:
return False
# check block
for i in range(3):
for j in range(3):
nx, ny = x // 3 * 3 + i, y // 3 * 3 + j
if nx != x and ny != y and board[nx][ny] == board[x][y]:
return False
return True
def sudoku_solver(board):
n = len(board)
for i in range(n):
for j in range(n):
if board[i][j] == 0:
for k in range(1, 10):
board[i][j] = k
if is_valid(board, i, j) and sudoku_solver(board):
return True
board[i][j] = 0
return False
return True
# realistic board
board = [[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 8, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 3, 6, 0, 0, 0, 0, 0],
[0, 7, 0, 0, 9, 0, 2, 0, 0],
[0, 5, 0, 0, 0, 7, 0, 0, 0],
[0, 0, 0, 0, 4, 5, 7, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 3, 0],
[0, 0, 1, 0, 0, 0, 0, 6, 8],
[0, 0, 8, 5, 0, 0, 0, 1, 0]]
sudoku_solver(board)
for row in board:
print(row)[1, 2, 4, 7, 3, 8, 6, 5, 9]
[6, 8, 5, 9, 1, 2, 3, 7, 4]
[7, 9, 3, 6, 5, 4, 8, 2, 1]
[3, 7, 6, 8, 9, 1, 2, 4, 5]
[4, 5, 9, 2, 6, 7, 1, 8, 3]
[8, 1, 2, 3, 4, 5, 7, 9, 6]
[5, 4, 7, 1, 8, 6, 9, 3, 2]
[2, 3, 1, 4, 7, 9, 5, 6, 8]
[9, 6, 8, 5, 2, 3, 4, 1, 7]https://web.stanford.edu/class/archive/cs/cs106b/cs106b.1208/lectures/fractals/Lecture10_Slides.pdf
Some recursive algorithms have overlapping subproblems.
F(n)=⎩⎨⎧01F(n−1)+F(n−2)if n=0(base case)if n=1(base case)if n>1(recursive case)
Let’s compute F(5): F(5)=F(4)+F(3)=(F(3)+F(2))+(F(2)+F(1))=((F(2)+F(1))+(F(1)+F(0)))+((F(1)+F(0))+F(1))=(((F(1)+F(0))+F(1))+(F(1)+F(0)))+((F(1)+F(0))+F(1))=(((1+0)+1)+(1+0))+((1+0)+1)=5
How many times do we compute F(2)? F(1)? F(0)?
To solve this, there are a few approaches: - Memoization: store the results of the subproblems in a table - Solve the problem iteratively (bottom-up) or using dynamic programming (not covered now)
CPU times: user 11.5 s, sys: 47.1 ms, total: 11.5 s
Wall time: 11.6 s102334155CPU times: user 14 µs, sys: 1e+03 ns, total: 15 µs
Wall time: 16 µs10233415511.6s vs 16 µs!
A recursive function is tail recursive when recursive call is the last thing executed by the function.
Non tail recursion version: factorial(n)={1n×factorial(n−1)if n=0(base case)if n>0(recursive case)
Tail recursion version:
factorial(n,acc)={accfactorial(n−1,n×acc)if n=0(base case)if n>0(recursive case)
Why is tail recursion important?
Some compilers and interpreters perform tail call optimization (TCO), which means that the recursive call is replaced with a jump to the start of the function. This optimization saves space on the call stack and improves performance.
Or in other words, tail recursion is as efficient as iteration.